The Bakery 解题报告（cf833b dp 带优化的dp 线段树）

2018-05-22

http://codeforces.com/contest/833/problem/B

本文迁移自老博客，原始链接为 https://lookas2001.com/the-bakery-%e8%a7%a3%e9%a2%98%e6%8a%a5%e5%91%8a/

NOTICE

推荐在写这道题前看看 HH 的项链 解题报告（SDOI 2009 线段树 排序 离线处理）

算法设计

拿到题，3分钟，这是一道动态规划。写码，调试，提交，一气呵成，最后发现在第4个点超时。转过头来看，发现在处理每一个状态的时候套着一个循环，导致整体算法复杂度 O(n ^ 3) 遂放弃。

最近学习了线段树，然后再看这道题，发现了这道题在求不同数字的个数的时候进行了很多不必要的重复运算，可以用线段树解决。

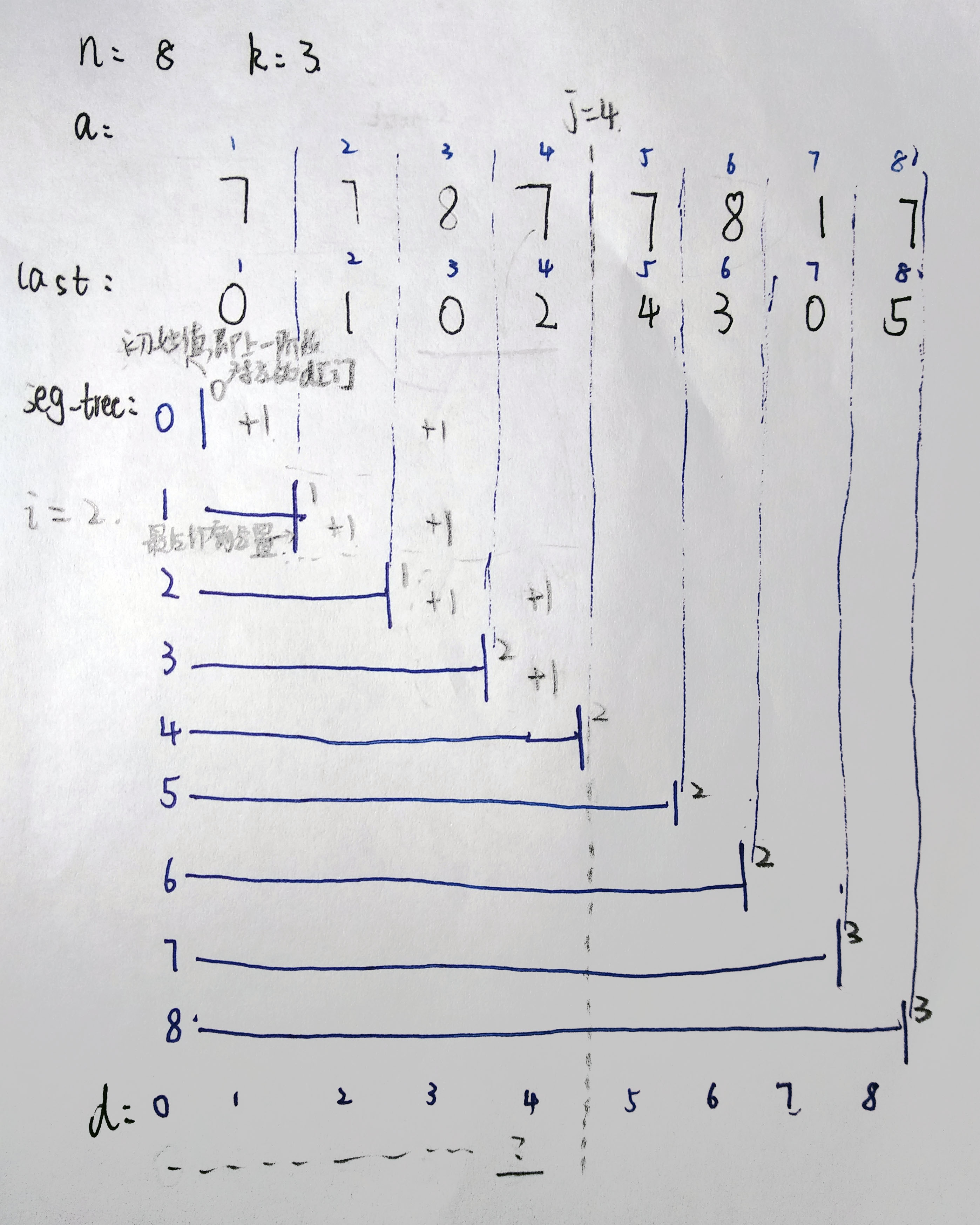
由于本人的描述实在不行，具体解决方案请直接看下面代码以及其注释，先粗略看一遍全局变量的定义，然后再看一下main函数。

配合这张图食用更佳。

示例代码

#include <cstdio>
#include <cstring>

const int N = 38500; // 35000 * 1.1

int n, k, a[N]; // 题目中提供的数据

int last[N]; // 记录该位置的数上一次出现的位置，last[i] 代表 a[i] 位置上的数在 a 数组中上一次出现的位置，如果没有出现过，则为 0
int index[N]; // 用于辅助建立 last 数组

int d[N]; // 动态规划中用于保留结果的数组， d[i] 代表在一次切割中（阶段），最后一个切割点（或者说是最后一个箱子装的最后一个蛋糕的坐标）的结果

struct node {
    int l, r;
    int f;
    int max;
    node *lc, *rc;
} mem[2 * N];
node *memp;
node *root; // 线段树中第 i 个位置的数 为 上一个阶段 d[i] 以及 i + 1 ~ j 中不同数字的个数 的和，其中 j 为当前推进到的位置，详见下方解释

inline void push_down(node *p) {
    if (p->f) {
        p->lc->max += p->f;
        p->lc->f += p->f; // mistake: 就像傻子一般，线段树这里给写错了
        p->rc->max += p->f;
        p->rc->f += p->f;
        p->f = 0;
    }
}

inline void pull_up(node *p) {
    if (p->lc->max > p->rc->max) p->max = p->lc->max; else p->max = p->rc->max;
}

node *init(int a[], int l, int r) {
    node *p = memp++;
    p->l = l;
    p->r = r;
    p->f = 0;
    if (l == r) {
        p->lc = p->rc = NULL;
        p->max = a[l];
    } else {
        int mid = (l + r) >> 1;
//      printf("%d %d %d\n", l, mid, r);
        p->lc = init(a, l, mid);
        p->rc = init(a, mid + 1, r);
        pull_up(p);
    }
    return p;
}

void change(node *p, int l, int r) {
    if (l <= p->l && p->r <= r) {
        ++p->max;
        ++p->f;
        return;
    }

    push_down(p);
    int mid = (p->l + p->r) >> 1;
    if (l <= mid) change(p->lc, l, r);
    if (mid < r) change(p->rc, l, r);
    pull_up(p);
}

int query(node *p, int l, int r) {
    if (l <= p->l && p->r <= r) {
        return p->max;
    }

    push_down(p);
    int mid = (p->l + p->r) >> 1;
    int max = 0, tmp;
    if (l <= mid) {
        max = query(p->lc, l, r);
    }
    if (mid < r) {
        tmp = query(p->rc, l, r);
        if (tmp > max) max = tmp;
    }
    pull_up(p); // mistake:这里的pull_up是不可或缺的

    return max;
}
//
//void debug2() {
//  for (int i = 1; i <= n; ++i) printf("%d ", last[i]);
//  printf("\n\n");
//}
//
//void debug1() {
//  for (int i = 0; i <= n; ++i) printf("%d ", d[i]);
//  printf("\n");
//}

int main() {
//  freopen("input.txt", "r", stdin);

    scanf("%d%d", &n, &k);
    memset(index, 0, sizeof index);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", a + i);
        last[i] = index[a[i]]; // 读取输入的过程中同时填充一下 last 数组，last 数组的含义见上定义
        index[a[i]] = i;
    }
//  
//  debug2();

    // 动态规划，为了能够对动态规划中的一个阶段中的不同状态下的求解能够快速进行，我们使用了递推，这样求解的顺序可以利用线段树进行优化
    memset(d, 0, sizeof d); // 不难发现最开始的结果都是 0 的
    for (int i = 1; i <= k; ++i) { // 阶段，即切割或者说是箱子的个数
        memp = mem;
        root = init(d, 0, n); // 线段树是可以从 0 开始建立的，详见下方解释
        for (int j = i; j <= n; ++j) { // 枚举当前阶段切割点的位置
            // 诚然，我们对于每一个切割点而言，我们都可以跑一次如下的循环
            /*
            int max = 0, tmp;
            for (int k = i - 1; k <= j - 1; ++k) { // 很明显 i - 1 之前的是不可能满足题意的
                tmp = last_d[k] + different_num_between(k, j);
                if (tmp > max) max = tmp;
            }
            */
            // 但是这样太慢了，我们发现，计算从 k 到 j 的有多少个不同的数字这个函数被调用了很多遍，并且发现貌似每次都进行了许多无用的计算
            // 我们建立一棵线段树，定义为当推进到 j 位置的时候，线段树中第 k 个数为从 k + 1（加一是为了初始化方便） 到 j 中不同数字的个数
            // 我们可以发现，last[j] + 1 到 j 中间是没有 a[j] 这个数的（一句废话）
            // 那也就是说，如果我们的进度推进到了 j 的话，对于所有的 在 last[j] + 1 ~ j 中的位置到 j 的不同数字种类应该会多出一个 j ，反映到数量上，就是个数 +1
            // 映射到线段树的时候别忘了位置 -1
            //  
            // 我们还可以发现，如果说按照上述定义，求最大值仍然需要扫描整个线段树，因为在原始的线段树上我们还需要增加上一个阶段的结果
            // 那么我们索性就在线段初始化的时候，将 d 数组作为线段树最开始的初始化用数组，这样求最大值就可以用线段树舒服的求出来了（当然线段树写错了当我没说）
            //
            // 被绕晕了？可以翻上去看看定义那里的注释，并且根据代码理解一下
            change(root, last[j] + 1 - 1, j - 1);
            d[j] = query(root, i - 1, j - 1); // mistake: 请注意，这里必须是 i - 1 而不是 i
        }
//      debug1();
    }
//  
//  // 哦，我的老伙计，这一坨被注释的代码是彻头彻底的错误
//  int max = 0;
//  for (int i = 1; i <= n; ++i) if (d[i] > max) max = d[i];
//  printf("%d", max);
//  for (int i = 1; i <= n; ++i) printf("%d ", d[i]);
//  printf("%d", d[n]);

    printf("%d", d[n]);

    return 0;
}